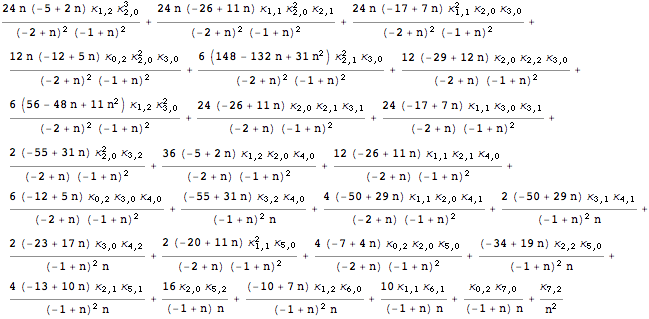Unbiased estimators of population moments
Moments of moments

mathStatica can find unbiased estimators of population moments. For instance, it offers h-statistics (unbiased estimators of population central moments), k-statistics (unbiased estimators of population cumulants), multivariate varieties of the same, polykays (unbiased estimators of products of cumulants) and much more.

Example:     k-statistics

Consider the k-statistic which is an unbiased estimator of the r^th cumulant ; that is, , for r = 1, 2, … .
Here are the 2^nd are 3^rd k-statistics:

In[1]:=

Out[1]=

Out[2]=

As per convention, the solution is expressed in terms of power sums .

Example:     Moments of moments

Because the above expressions (sample moments) are functions of random variables , we might want to calculate population moments of them. With mathStatica, we can find any moment (raw, central, or cumulant) of completley arbitrary expressions. For instance, is meant to have the property that . We test this by calculating the first raw moment of , and express the answer in terms of cumulants:

In[3]:=

Out[3]=

In 1928, Fisher published the product cumulants of the k-statistics, which are now listed in reference bibles such as Stuart and Ord (1994). Here is the solution to :

In[4]:=

Out[4]=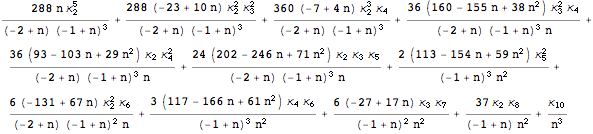

This is the correct solution. Unfortunately, the solutions given in Stuart and Ord (1994, equation (12.70)) and Fisher (1928) are actually incorrect.

Example:    Variance of the 3^rd sample central moment

Problem:  Find the variance of the 3^rd sample central moment .
Solution:  We proceed in two steps:

Step [1]: Express the 3^rd sample central moment in terms of power sums :

In[1]:=

Out[1]=

Step[2]: Since , the desired solution is simply the 2^nd Central Moment of .

In[2]:=

Out[17]=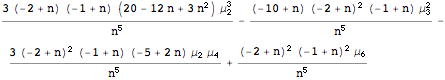

Problem:      Find  the covariance between   and    .
        Give the solution in terms of bivariate central moments of the population.

Solution:
We proceed in two steps:

Step [1]: Enter each expression in terms of bivariate power sums  .
      The first expression .   The second expression .

Step[2]: Since Cov(a, b) =  , the desired solution is simply:

In[1]:=

Out[1]=

Example:    Bring out the BFG           New in mathStatica 2.0

Cook (1951, pp.187–195) derived explicit results for product cumulants of various bivariate k-statistics; some of the simpler results are listed in Stuart and Ord (1994, Section 13.3). In this example, we illustrate not only how to obtain these known and published results, but more generally how one can obtain any such desired product cumulant … not just the simpler cases that are already known / published.

To illustrate, we will work here with the bivariate k-statistics and :

In[1]:=

Out[1]=

In[2]:=

Out[2]=

We will now find the product cumulant . In  the notation of Cook (1951, p.190) and Stuart and Ord (1994, equation (13.9)), this is the expression  :

In[3]:=

Out[3]=

Here is ;  in  the notation of Cook (1951, p.191), this is the expression :

In[4]:=

Out[4]=