|
Sum of Binomial and Poisson
Simon de Visscher <sdevisscher@hotmail.com> wrote:
> Do you have an idea about how to add a Poisson variable and a binomial?
Let  be independent of be independent of 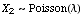 . We seek the distribution of the sum . We seek the distribution of the sum 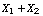 . .
Solution: Let 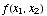 denote the joint pmf of denote the joint pmf of 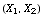 : :
![&nbs ... 955;^x_2)/x_2 ! ; domain[f] = {{x_1, 0, n}, {x_2, 0, ∞}} && {Discrete} ;](HTMLFiles/index_6.gif)
Let 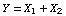 and and 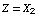 . Then the joint pmf of . Then the joint pmf of 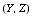 , say , say 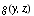 , is given by mathStatica's Transform function as: , is given by mathStatica's Transform function as:
![g = Transform[{y == x_1 + x_2, z == x_2}, f]](HTMLFiles/index_11.gif)
![(^(-λ) (1 - p)^(n - y + z) p^(y - z) λ^z Binomial[n, y - z])/z !](HTMLFiles/index_12.gif)
Deriving the domain of support of 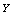 and and 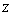 is a bit more tricky. The following diagram plots the space in the is a bit more tricky. The following diagram plots the space in the 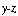 plane where plane where 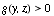 . .
![[Graphics:HTMLFiles/index_17.gif]](HTMLFiles/index_17.gif)
Then the domain of support (the shaded region in the figure) can be defined as follows:
When 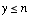 : : 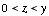
When 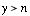 : : 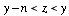
The pmf of 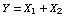 is then obtained by summing out is then obtained by summing out 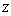 in each part of the domain: in each part of the domain:
* If 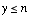 , the pmf of the sum , the pmf of the sum 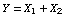 is: is:
![sol1 = Sum[Evaluate[g], {z, 0, y}]](HTMLFiles/index_26.gif)
![(^(-λ) (1 - p)^(n - y) p^y Γ[1 + n] Hypergeometric1F1[-y, 1 + n - y, ((-1 + p) λ)/p])/(Γ[1 + n - y] Γ[1 + y])](HTMLFiles/index_27.gif)
* If 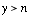 , the pmf of the sum , the pmf of the sum 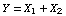 is: is:
![sol2 = Sum[Evaluate[g], {z, y - n, y}]](HTMLFiles/index_30.gif)
![(^(-λ) p^n λ^(-n + y) Hypergeometric1F1[-n, 1 - n + y, ((-1 + p) λ)/p])/Γ[1 - n + y]](HTMLFiles/index_31.gif)
where Hypergeometric1F1[a, b, z] denotes the Kummer confluent hypergeometric function 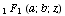 . .
| 

