Torben Hoffmann <Torben.Hoffmann@mo-to-ro-la.com> wrote:

... The sum of _many_ beta distributions converges to a gaussian distribution, but neither my beloved book (and some hard core integral solving) or extensive search on the internet has given me anything on what the distribution of the sum of two beta functions is ...

Given:
Let X1 and X2 be independent random variables, each distributed as Beta(a, b).   Let   f(x1, x2)   denote the joint pdf of (X1, X2):

In[1]:=


Solution 1: MGF Method

The characteristic function (cf) of Y = X1 + X2 is:

In[2]:= cf = Expect[Exp[t (x_1 + x_2))], f]
Out[2]= Hypergeometric1F1[a, a + b, i t]^2

Inverting the cf symbolically fails to yield a solution here. However, for given parameter values, we can invert the cf numerically using mathStatica's NInvertCF function. For example, if a = 1 and b = 2, we obtain a plot of the pdf of X1 + X2 via:

In[3]:=

Fig. 1: Plot of the pdf of X1 + X2, when Xi ~ Beta(1, 2)

Clearly, a Normal approximation would generally be most inappropriate for the sum of 2 Betas.


Solution 2: Transform Method

Let  Y = X1 + X2  and  Z = X2. Then the joint pdf of (Y, Z), say g(y, z), is obtained with mathStatica's Transform function:

In[1]:=

Out[1]=

Deriving the domain of this joint pdf is a bit more tricky, but can be assisted by using mathStatica's DomainPlot function which plots the space in the y-z plane where g(y, z) > 0:

In[2]:=


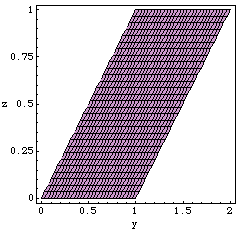
Fig. 2: The space in the y-z plane where g(y, z) > 0

We see that the domain (the shaded region) can be defined as follows:

  • When y < 1:     0  <  z  <  y
  • When y > 1:     y  <  1+z  <  2   or equivalently   y – 1  <  z  <  1

The density of Y = X1 + X2 is then obtained by integrating out Z in each part of the domain. The following function does the job for us, given parameters a and b:

In[3]:=

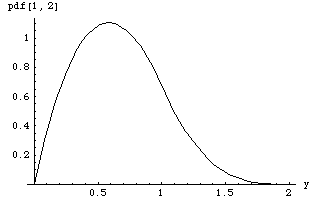
That's it. We can now find exact symbolic solutions for the pdf of Y = X1 + X2 given parameter values a and b. Three examples illustrate:

Example 1: Here we derive the pdf of Y = X1 + X2, when a = 1 and b = 2 (but now as a closed form exact solution):

In[4]:= pdf[1, 2]
Out[4]=

Plot of the pdf of Y when a = 1 and b = 2:

In[5]:=


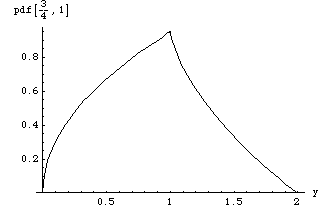
Example 2: a = ¾, b = 1

In[6]:= pdf[3/4, 1]
Out[6]=       

Plot of the pdf:

In[7]:=


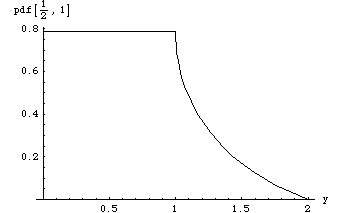
Example 3: a = ½, b = 1

In[8]:= pdf[1/2, 1]
Out[8]=

Plot of the pdf:

In[9]:=